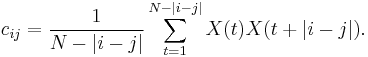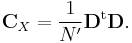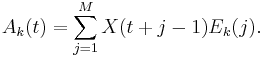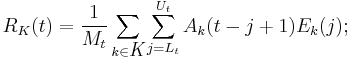Singular spectrum analysis

Singular spectrum analysis (SSA) combines elements of classical time series analysis, multivariate statistics, multivariate geometry, dynamical systems and signal processing. Its roots lie in the classical Karhunen (1946)–Loève (1945, 1978) spectral decomposition of time series and random fields and in the Mañé (1981)–Takens (1981) embedding theorem.

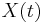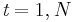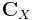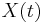In practice, SSA is a nonparametric spectral estimation method based on embedding a time series X(t): {\textit t=1,N} in a vector space of dimension M. SSA proceeds by diagonalizing the M\times M lag-covariance matrix {\textbf C}_X of X(t) to obtain spectral information on the time series, assumed to be stationary in the weak sense. The matrix 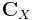{\textbf C}_X can be estimated directly from the data as a Toeplitz matrix with constant diagonals (Vautard and Ghil, 1989), i.e., its entries 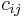c_{ij} depend only on the lag |i-j|:

c_{ij} = \frac{1}{N-|i-j|} \sum_{t=1}^{N-|i-j|} X(t) X(t%2B|i-j|).

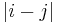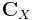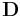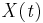An alternative way to compute {\textbf C}_X, is by using the N' \times M ``trajectory matrix" {\textbf D} that is formed by M lag-shifted copies of {\it X(t)}, which are N' =N-M%2B1 long; then

{\textbf C}_X = \frac{1}{N'} {\textbf D}^{\rm t} {\textbf D}.

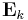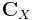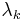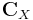The M eigenvectors {\textbf E}_k of the lag-covariance matrix {\textbf C}_ X are called temporal empirical orthogonal functions (EOFs). The eigenvalues \lambda_k of {\textbf C}_{X} account for the partial variance in the direction 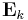{\textbf E}_k and the sum of the eigenvalues, i.e., the trace of 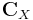{\textbf C}_{X}, gives the total variance of the original time series 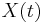X(t). 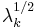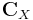The name of the method derives from the singular values \lambda^{1/2}_k of {\textbf C}_{X}.

Contents

Decomposition and reconstruction

Projecting the time series onto each EOF yields the corresponding temporal principal components (PCs) 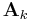{\textbf A}_k:

A_k(t) = \sum_{j=1}^{M} X(t%2Bj-1) E_k(j).

An oscillatory mode is characterized by a pair of nearly equal SSA eigenvalues and associated PCs that are in approximate phase quadrature (Ghil et al., 2002). Such a pair can represent efficiently a nonlinear, anharmonic oscillation. 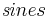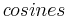This is due to the fact that a single pair of data-adaptive SSA eigenmodes often will capture better the basic periodicity of an oscillatory mode than methods with fixed basis functions, such as the {\textit sines} and {\textit cosines} used in the Fourier transform.

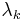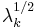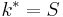The window width M determines the longest periodicity captured by SSA. Signal-to-noise separation can be obtained by merely inspecting the slope break in a "scree diagram" of eigenvalues \lambda_k or singular values \lambda^{1/2}_k vs. k. The point k^* = S at which this break occurs should not be confused with a ``dimension" D of the underlying deterministic dynamics (Vautard and Ghil, 1989).

A Monte-Carlo test (Allen and Robertson, 1996) can be applied to ascertain the statistical significance of the oscillatory pairs detected by SSA. The entire time series or parts of it that correspond to trends, oscillatory modes or noise can be reconstructed by using linear combinations of the PCs and EOFs, which provide the reconstructed components (RCs) 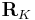{\textbf R}_K:

R_{ K}(t) = \frac{1}{M_t} \sum_{k\in {\textit K}} \sum_{j={L_t}}^{U_t} A_k(t-j%2B1)E_k(j);

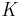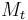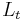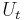here \textit K is the set of EOFs on which the reconstruction is based. The values of the normalization factor M_t, as well as of the lower and upper bound of summation L_t and U_t, differ between the central part of the time series and the vicinity of its endpoints (Ghil et al., 2002).

Multivariate extension

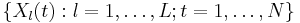Multi-channel SSA (or M-SSA) is a natural extension of SSA to an L-channel time series of vectors or maps with N data points \{X_{l}(t): l=1,\dots, L; t=1,\dots, N\}. In the meteorological literature, extended EOF (EEOF) analysis is often assumed to be synonymous with M-SSA. The two methods are both extensions of classical principal component analysis (PCA) but they differ in emphasis: EEOF analysis typically utilizes a number L of spatial channels much greater than the number M of temporal lags, thus limiting the temporal and spectral information. 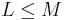In M-SSA, on the other hand, one usually chooses L \leq M. Often M-SSA is applied to a few leading PCs of the spatial data, with M chosen large enough to extract detailed temporal and spectral information from the multivariate time series (Ghil et al., 2002).

Spatio-temporal gap filling

The gap-filling version of SSA can be used to analyze data sets that are unevenly sampled or contain missing data (Kondrashov and Ghil, 2006). For a univariate time series, the SSA gap filling procedure utilizes temporal correlations to fill in the missing points. For a multivariate data set, gap filling by M-SSA takes advantage of both spatial and temporal correlations. In either case: (i) estimates of missing data points are produced iteratively, and are then used to compute a self-consistent lag-covariance matrix 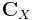{\textbf C}_X and its EOFs 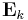{\textbf E}_k; and (ii) cross-validation is used to optimize the window width M and the number of leading SSA modes to fill the gaps with the iteratively estimated "signal," while the noise is discarded.

Brief history

Broomhead and King (1986a, b) proposed to use SSA and M-SSA in the context of nonlinear dynamics for the purpose of reconstructing the attractor of a system from measured time series. These authors provided an extension and a more robust application of the Mañé (1981)-Takens (1981) idea of reconstructing dynamics from a single time series.

Ghil, Vautard and associates (Vautard and Ghil, 1989; Ghil and Vautard, 1991; Vautard et al., 1992) noticed the analogy between the trajectory matrix of Broomhead and King, on the one hand, and Karhunen (1946)-Loève (1945) principal component analysis in the time domain, on the other. Thus, SSA can be used as a time-and-frequency domain method for time series analysis — independently from attractor reconstruction and including cases in which the latter may fail.

At present, the papers dealing with the methodological aspects and the applications of SSA number in the hundreds. Introductions to and reviews of the literature are provided by Elsner and Tsonis (1996), Danilov and Zhigljavsky (1997), Golyandina et al. (2001), and Ghil et al. (2002). Recently it is been used for tool condition monitoring and bearing fault detection.

References

See also

External links